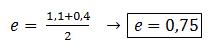LAMBE, T. William. y WHITMAN, Robert V. Mecanica de Suelos. Mexico: Limusa, 2009. p. 42, 43, 46, 47, 49, 163, 169, 171, 180, 304, 337, 343, 430, 435
Las formulas y las tablas en las que nos basamos para realizar este blog fueron seleccionadas del libro que acabamos de referenciar.
miércoles, 17 de noviembre de 2010
ESTABILIDAD DEL TALUD (GEOSLOPE)
Para poder analizar la estabilidad del talud en el programa GeoSlope se realizó una simplificacion de las discontinuidades en las pendientes de este, se halló una pendiente global del talud trazando un triángulo con los puntos extremos de este obteniendo un ángulo de inclinación de 58°.
Los datos utilizados para correr el programa fueron:
Unit Weight: 18.21 kN/m³
Cohesion: 20 kPa
Phi: 26 °
Una vez corrido el programa, analizando el talud con los métodos de Janbu, Bishop y el Ordinario, se obtuvo la siguiente superficie de falla con sus respectivos factores de seguridad.
Como vemos, la falla es en circulo de pie, esto es debido a que β > 53°
Factores de seguridad calculados por Geoslope:
El método de Janbu es el que menor Factor de Seguridad presenta, ya que este método no tiene en cuenta que existe equilibrio de momentos, podríamos decir que es menos confiable que el método de Bishop el cual considera equilibrio tanto de momentos como de fuerzas verticales.
Estos dos métodos se realizan por medio de procesos iterativos, por lo cual podríamos decir que muestra valores más reales del FS que el método ordinario.
Como era de esperarse, el método de Bishop por lo general muestra valores para el FS mayores que el método Ordinario y de Janbu.
Con estos Factores de Seguridad encontrados, analíticamente al ser valores menores que 1 se podría decir que el talud es inestable por sí mismo y debe fallar, y comparando estos resultados con lo visto en este talud, podemos concluir que estos métodos son acertados ya que el talud realmente colapso.
sábado, 13 de noviembre de 2010
PROPIEDADES MECANICAS DEL SUELO
ANGULO DE FRICCION
Limo no plástico
Para la resistencia residual Φcv = 26°
LAMBE. Pag 163
COHESION
COEFICIENTE EMPUJE DE TIERRAS ACTIVO (ka) Y PASIVO (kp)
Para Φ = 26° ka = 0,406 kp = 2,46
LAMBE. Pag 180
MODULO DE YOUNG
LAMBE. Pag 169
Esta tabla relaciona el Modulo de Young (E) con la Compacidad relativa (Dr) del suelo
Una relación de vacios baja implica que el modulo de Young tenga un valor elevado, por lo tanto seleccionamos el segundo intervalo de esfuerzos
Una relación de vacios baja implica que el modulo de Young tenga un valor elevado, por lo tanto seleccionamos el segundo intervalo de esfuerzos
Para: Dr = 0 E = 1,8 kg/m2
COEFICIENTE DE CONSOLIDACION (Cv)
Para un WL = 44,9%
§ Cv = 3,3x10-3 cm2/seg En la zona virgen
§ Cv = 7,5x10-4 cm2/seg En la zona de fluencia
LAMBE. Pag 435
γw = 10 kN/m3
k = 2,5x10-10 m/seg
Cv1 = 3,3x10-7 m2/seg mv1 = 7,6x10-5 m2/kN
Cv2 = 7,5x10-8 m2/seg mv2 = 3,33x10-4 m2/kN
Los valores que encontramos del coeficiente de deformación volumétrica (mv) son muy bajos, por lo tanto los valores del Modulo con confinamiento (D) van a tener valores muy altos, al ser inversamente proporcionales.
D1 = 13200 kPa
D2 = 3000 kPa
COEFICIENTE DE COMPRESIBILIDAD
av = (1+e0) mv
e0 = enatural = 0,75
av1 = 1,33x10-4 m2/kN
av2 = 5,78x10-4 m2/kN
INDICE DE COMPRESIÓN (Cc)
Para suelo remoldeado: Cc = 0,007(WL-10)
Cc = 0,244
INDICE DE EXPANSIÓN (Cs)
Cs = 0,0463(Gs) WL/100
Cs = 0,056
La siguiente ecuación relaciona el Modulo con confinamiento con el Modulo de Young partiendo del coeficiente de Poisson (μ)
Como ya tenemos los valores de D y E al despejar μ nos queda:
El coeficiente de Poisson nos va dar μ = 0,74 reemplazando D por cualquiera de sus valores y E = 4,75 kPa
VALORES TIPICOS DEL SUELO
LAMBE. Pag 43
ACTIVIDAD

RELACION DE VACIOS
emáx = 1,1 emin = 0,4
POROSIDAD
nmáx = 52% nmin = 29%

PESO ESPECIFICO SECO APARENTE
γdmáx = 1,89 ton/m3 γdmin = 1,28 ton/m3
Los valores anteriores fueron seleccionados de la Tabla 3,2. Con los valores maximo y minimo de un Limo inorganico sacamos un promedio, y tomamos este como el valor para el ML
PERMEABILIDAD
LAMBE. Pag 304
Para el limo de Boston se tienen permeabilidades con relacion de vacios entre 0,75 y 1,1
Para una e=0,75 el suelo es prácticamente impermeable, como es nuestro ML
k = 2,5x10-8 cm/seg
NOMBRES TIPICOS Y ALGUNAS PROPIEDADES IMPORTANTES
NOMBRES TIPICOS PARA UN ML
§ Limos orgánicos
§ Arenas muy finas
§ Polvo de roca
§ Arenas finas limosas
§ Arenas finas arcillosas con cierta plasticidad
Lambe. Pag 49
Permeabilidad en estado compacto: Semipermeable a impermeable
Resistencia al corte en estado compacto y saturado: Regular
Compresibilidad en estado compacto y saturado: Media
RESUMEN DATOS SUELO DE CALDAS
Nuestro trabajo esta basado en el blog http://suelodecaldas.blogspot.com. El cual es un Limo de Baja Compresibilidad (ML) a continuacion veremos los datos en los cuales nos basaremos para deducir algunas propiedades del suelo:
DISTRIBUCION GRANULOMETRICA
DISTRIBUCION GRANULOMETRICA
GEOMETRIA DEL TALUD ORIGINAL
La altura total del talud es de 7,16 m, y el suelo fue retirado de una altura de 5,66 m respecto al nivel del terreno
Gs = 2,68
La altura total del talud es de 7,16 m, y el suelo fue retirado de una altura de 5,66 m respecto al nivel del terreno
Gs = 2,68
Suscribirse a:
Comentarios (Atom)